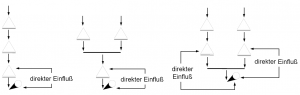
Betriebsregeltypen
Der Betriebsplan einer Talsperre oder eines Speicherverbundsystems liegt normalerweise in Form einer textlichen oder grafischen Ausfertigung vor und ist häufig Bestandteil der Planfeststellung der Gesamtanlage. Die Komplexität eines Betriebsplanes kann sehr unterschiedlich sein. So reicht die Spanne von einer einfachen Festlegung von Hochwasserschutzräumen und der zusätzlichen Aufstellung eines Melde- und Alarmplans zur Benachrichtigung der Aufsichtsbehörden in Ausnahmesituationen, bis zu komplexen Regelwerken in Form von funktionalen Abhängigkeiten, die aus verschiedenen Systemzuständen die Abgaben ableiten.
Nachfolgend sind Beispiele aufgeführt, welche die Vielfalt möglicher Vorschriften und die Reduzierung auf die wesentlichen Abhängigkeiten deutlich machen sollen. Daraus wird ein Konzept abgeleitet, wie die Mehrzahl der Betriebsregeln durch wenige grundsätzliche Rechenvorschriften abgebildet werden können. Die gegebene Auswahl besitzt nicht den Anspruch auf Vollständigkeit, jedoch dürfte der größte Teil der in der Praxis angewendeten Regeln enthalten sein.
Grundsatz: Überprüfung physikalischer Grenzen
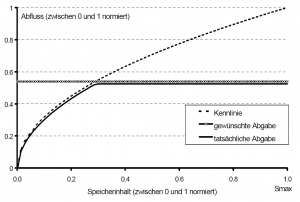
Bei der Festlegung von Abgaben gemäß einer Betriebsregel wird vorausgesetzt, dass die Kapazität der Auslässe zur Erfüllung der Abgaben ausreichend groß ist. Somit müssen bei der Dimensionierung der Auslassorgane die Vorgaben des wasserwirtschaftlichen Betriebs Berücksichtigung finden. In der Regel wird es in dieser Hinsicht keinerlei Probleme geben. Grundsätzlich steht jedoch die physikalisch machbare Abgabe, durch die Kennlinie der Auslässe bei voller Öffnung gegeben, als oberer Grenzwert fest.
Reicht die Druckhöhe bzw. die Kapazität des Auslasses bei voller Öffnung aus, um die gewünschte Menge abzugeben, kann durch Schließen eines Schiebers die Abgabe auf das vorgesehene Maß gedrosselt werden. Reicht die Druckhöhe nicht aus, ist nur die hydraulisch mögliche Abgabe erreichbar.
- Mathematische Abstraktion:
- Alle Abgaben gemäß einer Betriebsregel sind Funktionen des Speicherinhaltes und können die maximale Kapazität der Auslässe bei voller Öffnung nicht überschreiten. Sobald das Leistungsvermögen der Auslassorgane die geforderte Abgabenmenge übersteigt, kann diese durch partielles Schließen der Regelorgane eingestellt werden.
Alle nachfolgend erwähnten Formen von Abgaben aus Speichern unterliegen dieser Einschränkung.
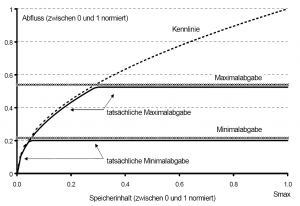
Regel Typ 1: Festlegung einer Mindestabgabe oder einer im Unterlauf schadlos abführbaren Maximalabgabe.
- Abhängigkeit:
- Die Festlegung einer Mindest- oder einer Maximalabgabe ergibt sich aufgrund von Anforderungen im Unterlauf eines Speichers. Die Maximalabgabe orientiert sich oft am bordvollen Abfluss eines kritischen, unterhalb liegenden Gewässerquerschnittes. Für ihre Bestimmung existiert folglich ein eindeutiges hydraulisches Verfahren. Im Gegensatz dazu besteht für die Mindestabgabe keine klare Richtlinie. Häufig kommen bestimmte Verhältnisse von MNQ oder MQ zum Ansatz. Unabhängig von der Ermittlung der Mindest- oder Maximalabgabe gilt jedoch das zuvor als Grundsatz beschriebene Prinzip der Abhängigkeit vom Leistungsvermögen der Auslassorgane. Minimal- und Maximalabgabe können nur abgelassen werden, wenn bei der gegebenen Druckhöhe die Kapazität der Auslässe ausreicht. Da es in der Praxis wohl kaum vorkommen wird, das sich die Dimensionierung der Auslassorgane und die geforderten Abgaben widersprechen, ist der Hinweis auf die Abhängigkeit vom Speicherinhalt eher theoretischer Art, für die Ableitung allgemeiner Gesetzmäßigkeiten aber notwendig.
- Mathematische Abstraktion:
- Minimal- und Maximalabgabe sind Funktionen des Speicherinhaltes und folgen bei sehr geringer Füllung der Kennlinie vollgeöffneter Auslässe. Sobald die Kapazität der Auslassorgane für die geforderte Abgabemenge ausreicht, kann die Abgabe durch partielles Schließen der Regelorgane konstant gehalten werden.
Regel Typ 2: Einhalten eines Hochwasserschutzraumes, evtl. zeitlich variabel über das Jahr
- Abhängigkeit:
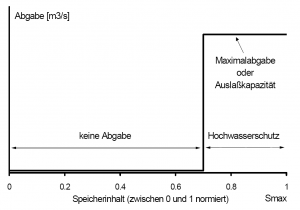
- Die Festlegung eines Hochwasserschutzraumes beinhaltet als Minimalanforderung nur die Benennung eines Volumens, welches für die Aufnahme von Hochwasser im Speicher freizuhalten ist. Die Dimensionierung erfolgt auf der Basis von Hochwasserfüllen mit bestimmten Wiederkehrintervallen. Überschreitet der Wasserstand die Marke des Schutzraums wird durch eine erhöhte Abgabe an den Unterlauf für das Freiräumen gesorgt. Somit reduziert sich diese Vorschrift auf eine Beziehung zwischen Abgabe und Speicherinhalt, wobei als erhöhte Abgabe zum Freihalten die Auslasskapazität oder ein definierter Maximalabfluss als obere Grenze dienen kann. Ist der Hochwasserschutzraum über das Jahr zeitlich variabel, so ändert sich nur der Speicherinhalt ab dem die Abgabe erhöht wird.
- Mathematische Abstraktion:
- Hier existiert eine direkte Beziehung zwischen Speicherinhalt und Abgabe. Überschreitet der Speicherinhalt die Marke des Hochwasserschutzraums, so erfolgt eine Abgabe, bleibt er unterhalb der Marke wird die Abgabe zu Null gesetzt.
Regel Typ 3: Direkte Trink- oder Brauchwasserentnahmen aus einem Speicher
- Abhängigkeit:
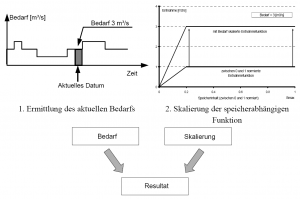
- In erster Linie bestimmt der aktuelle Bedarf die Entnahme aus dem Speicher, wobei er im Allgemeinen zeitlichen Schwankungen unterliegt. Nach oben wird der Bedarf häufig durch Wasserrechte bzw. maximale Entnahmemengen eingegrenzt, die sich auf ausgewählte Zeithorizonte wie Tag, Monat, Vierteljahr, Jahr oder andere beziehen. Betrachtet man zunächst nur den aktuellen Bedarf, so ist dieser durch die Anforderungen eines Wasserversorgers festgelegt und definiert den Anspruch an den Speicher. Ein Bezug zum Speicherinhalt besteht nicht. Ob der Anspruch tatsächlich erfüllt werden kann ist jedoch vom aktuellen Speicherinhalt abhängig. Diese Bindung ist entweder durch die bauliche Struktur der Entnahmeeinrichtung oder aus Gründen einer vorausschauenden Bewirtschaftung gegeben. So ist z.B. beim Erreichen besonders geringer Speicherfüllungen das rechtzeitige Drosseln der Entnahmen sinnvoll, um ein Leerlaufen des Speichers und damit ein völliges Versagen in längeren Niedrigwasserperioden zu vermeiden[1]. Aus diesem Grund gibt es normalerweise in jeder hauptsächlich der Trinkwasserversorgung dienenden Talsperre einen Reserveraum, über dessen Nutzung i.d.R. Sonderbetriebspläne entscheiden.
- Mathematische Abstraktion:
- Ist der Bedarf genau bekannt und unveränderlich, kann eine direkte Beziehung zwischen Entnahme und Speicherinhalt definiert werden. Normalerweise ist aber der Bedarf bestimmten Schwankungen unterworfen. Aus diesem Grund empfiehlt es sich, die Beziehung Entnahme/Speicherinhalt zu normieren, wobei der aktuelle Bedarf als Skalierungsfaktor dient. Unterschreitet der Speicherinhalt einen definierten Grenzwert, wird nur noch ein bestimmter Prozentsatz des aktuellen Bedarfs befriedigt. Der Grenzwert sowie die Form der Funktion können zeitlich variabel sein.
Regel Typ 4: Regelabgabe in den Unterlauf
- Abhängigkeit:
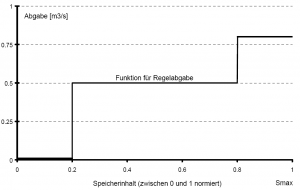
- Die Regelabgabe in den Unterlauf sorgt für einen Abflussausgleich in bezug auf saisonale Unterschiede des Zuflusses. Ist eine Mindestabgabe vorgeschrieben, so wird diese in der Regelabgabe enthalten sein. Zur Beschreibung der Regelabgabe dient häufig ein Lamellenplan. Dieser unterteilt den Speicherinhalt in verschiedene Bereiche (Lamellen) und ordnet jeder Lamelle eine Abgabe zu. Bei der Bestimmung des Lammellenplans spielt das langjährige Abflussgeschehen und die sonstigen Entnahmen aus dem Speicher zu anderen Zwecken eine entscheidende Rolle. Ein Speicher soll in zuflussstarken Zeiten Wasser sammeln aber trotzdem nicht überlaufen, um in zuflussschwachen Perioden ausreichend Reserven zu besitzen. Die Kopplung der Abgaben an die Speicherlamellen ist eine eindeutige Funktion des Speicherinhaltes. Da auf innerjährliche Zuflussschwankungen reagiert werden soll, sind zeitlich veränderliche Beziehungen zwischen Inhalt und Abgabe die Regel.
- Mathematische Abstraktion:
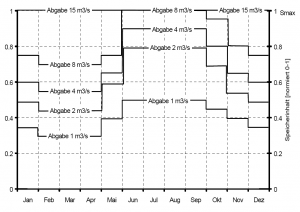
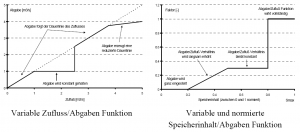
- Wie in den vorangegangenen Regeln trifft auch hier zu, dass die Abgabe vom Speicherinhalt abhängig ist. Üblicherweise erfolgt die Wiedergabe eines Lamellenplanes in einem zweidimensionalen Diagramm. Auf der X-Achse ist die Zeit eines Jahres aufgetragen, auf der Y-Achse der Speicherinhalt. In das Diagramm sind als Linien gleicher Abgaben die Lamellen eingezeichnet.
- Eine solche Ansicht ist zwar praktisch aber noch nicht vollständig, wie sich nachfolgend zeigen lässt. Durch eine dreidimensionale Darstellung eines einfachen Lamellenplans wird dies deutlich. Auf der X- Achse ist die Zeit, auf der Y-Achse der Speicherinhalt aufgetragen, während die Z-Achse die Abgabe nach oben gerichtet anzeigt.
- Das 3D-Bild senkrecht von oben betrachtet ergibt wieder die zweidimensionale Form. Anstatt konstante Blöcke für die einzelnen Zeithorizonte zu nehmen, tritt auch häufig der Fall einer linearen Verbindung auf.
- Für die einzelnen Zeitabschnitte - hier Monate - kommen unterschiedliche funktionale Abhängigkeiten zwischen Speicherinhalt und Abfluss zum Tragen. Betrachtet man für einen ausgewählten Zeitpunkt die Speicherinhalt/Abgaben Beziehung, so bleiben zwei Möglichkeiten die Knotenpunkte der Abgaben zu verbinden. Zum einen besteht die Möglichkeit einer linearen Interpolation, zum anderen sind aber genauso Treppenstufen möglich.
- Im zweidimensionalen Raum ist diese Information nicht sichtbar und muss extra angegeben werden. Es besteht aber meistens die Konvention, Abgaben zwischen zwei Knotenpunkten als konstant anzunehmen, also den Lamellenplan wie oben gezeigt in Form von Treppenstufen zu interpretieren.
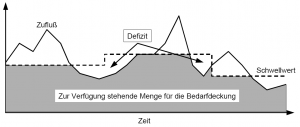
Regel Typ 5: Einhalten definierter Abflüsse im Unterlauf von Speichern (Niedrigwasseraufhöhung / Bedarfsdeckung)
- Abhängigkeit:
- In diesem Fall ist die momentane Abgabe durch Anforderungen aus dem Unterlauf eines Speichers bestimmt. An einem Gewässerquerschnitt im wasserwirtschaftlichen System, der im weiteren Verlauf Kontrollstelle genannt wird und durch Speicherabgaben beeinflusst ist, soll ein definierter Abfluss nicht unterschritten werden. Der Abfluss an der Kontrollstelle setzt sich aus der Abgabe aus Speichern und den dazwischen liegenden seitlichen Zuflüssen zusammen. Bleibt der aktuelle Abfluss unterhalb der Sollgröße, wird ein Zuschuss aus oberhalb liegenden Speichern notwendig. Die Höhe des Zuschusses richtet sich nach der Differenz zwischen Sollabfluss und tatsächlichem Abfluss. Ob der geforderte Zuschuss aus dem Speicher vollständig erbracht werden kann, ist wiederum vom aktuellen Speicherinhalt abhängig, denn je niedriger die Speicherfüllung ist, um so ungünstiger ist es, zusätzliches Wasser abgeben zu müssen. Insofern verhält sich die Niedrigwasseraufhöhung/Bedarfsdeckung vollkommen analog zur Trink-oder Brauchwasserentnahme, lediglich der auslösende Faktor unterscheidet sich. Wie zuvor erfolgt auch hier eine Skalierung einer speicherabhängigen Funktion durch einen Faktor, der sich nun allerdings aus einem Vergleich zwischen Sollwerten und aktuellen Abflüssen ergibt.
- Mathematische Abstraktion:
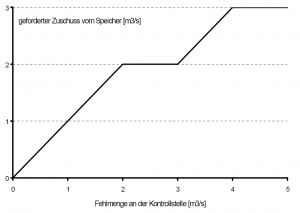
- Die Ermittlung der Abgabe zur Niedrigwasseraufhöhung bzw. Bedarfsdeckung an Kontrollstellen setzt sich aus mehreren Faktoren zusammen. Auf der einen Seite ergibt sich eine in ihrer Größe wechselnde Fehlmenge durch Unterschreiten eines geforderten Sollabflusses. Wie diese Fehlmenge als Skalierungsfaktor auf eine Speicherabgabe wirken soll, lässt sich über eine funktionale Beziehung definieren. Dabei fungiert die Fehlmenge als unabhängige, der Skalierungsfaktor als abhängige Größe.
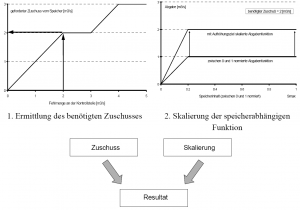
- Auf der anderen Seite ist es eine Frage der aktuellen Speicherfüllung, ob und gegebenenfalls wie dem geforderten Zuschuss aus dem Speicher entsprochen werden kann. Wie zuvor führt eine normierte speicherabhängige Funktion zusammen mit dem angeforderten Bedarf zu einer eindeutigen Bestimmung der Zuschussmenge. In der folgenden Abbildung 10 ist eine vollständige Deckung des Aufhöhungziels bzw. des Bedarfs nur dann zu erreichen, wenn der Speicherinhalt über einem kritischen Grenzwert von ca. 25% Füllungsgrad liegt.
- Besitzen mehrere Speicher Einfluss auf die maßgebende Kontrollstelle oder sollen prinzipiell mehrere Speicher zur Bedarfsdeckung herangezogen werden, so ist der benötigte Zuschuss gemäß einer entsprechenden Vorschrift auf die Speicher aufzuteilen. Dabei ist zwischen direktem und indirektem Einfluss eines Speichers auf die Kontrollstelle zu unterscheiden. Ein direkter Einfluss liegt immer dann vor, wenn die Speicherabgabe unmittelbar auf den Abflusszustand am Kontrollpunkt einwirken kann, d.h. zwischen Speicher und Kontrollstelle kann das natürliche Fließverhalten nicht mehr durch regulierende Eingriffe verändert werden. Ist dies nicht der Fall ist ein indirekter Einfluss gegeben.
- Alle Speicher mit direktem Einfluss auf die Kontrollstelle erhalten jeweils eine Fehlmengen/Faktor- und eine inhaltsabhängige skalierbare Funktion gemäß Abbildung 10. Dadurch kann in Abhängigkeit von Fehlmenge und Speicherinhalt die tatsächlich getätigte Abgabe für jeden Speicher separat bestimmt werden.
Regel Typ 6: Abgabe in Abhängigkeit des aktuellen Speicherzuflusses
- Abhängigkeit:
- Hier erfolgt eine direkte Kopplung zwischen Abgabe und aktuellem Zufluss zum Speicher. Ähnlich wie beim Lamellenplan handelt es sich ebenfalls um eine Anpassung an unterschiedliche Zuflusssituationen. Dies geschieht zur Verhinderung des Leer- oder Überlaufens oder um ein variables Abflussregime im Unterlauf zu erhalten. Langfristige Zuflussschwankungen sind mit dieser Betriebsregel allerdings schwer zu erfassen, da nur Momentbetrachtungen durchgeführt werden.
- Zur endgültigen Bestimmung einer zuflussabhängigen Abgabe sind mehrere Komponenten zu berücksichtigen. Zuerst muss eine Beziehung zwischen aktuellem Zufluss und Abgabe vorhanden sein. Außer dem aktuellen Zufluss spielt aber auch der momentane Speicherinhalt eine wichtige Rolle, da die Beziehung Zufluss/Abgabe nicht über den gesamten Speicherinhalt hinweg uneingeschränkte Gültigkeit besitzen muss. So ist es sehr wahrscheinlich, dass bei Unterschreitung einer kritischen Speicherfüllung (z.B. eiserner Bestand) die Beziehung ganz aufgegeben wird oder zumindest die Abgabenmengen reduziert werden.
- Weil es bei dieser Regel zum Aufeinandertreffen von relativ geringen Speicherfüllungen bei gleichzeitig hohem Zufluss – und dadurch einer geforderten hohen Abgabe - kommen kann, muss dem Grundsatz der Überprüfung physikalischer Grenzen besondere Aufmerksamkeit gewidmet werden.
- Mathematische Abstraktion:
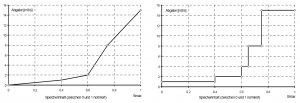
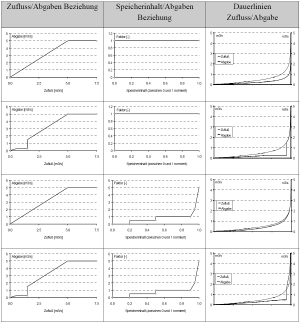
- In diesem Fall spielen drei funktionale Abhängigkeiten eine Rolle. Zum einen existiert eine direkte Funktion zwischen aktuellem Zufluss und der Abgabe. Die Form der Funktion kann beliebig sein. Es ist vorstellbar nur einzelne Bereiche des Zuflusses nachzubilden, was einer partiellen Angleichung der Abgabe an die Dauerlinie des Zuflusses entspricht.
- Zum anderen kann die Zufluss/Abgaben Funktion durch eine Beziehung zwischen Speicherinhalt und Abgabe überlagert werden. Aus Gründen der Übersichtlichkeit empfiehlt es sich, mit einer normierten Funktion zu arbeiten. Dadurch besteht entlang des gesamten Speicherinhaltes die Möglichkeit, das Resultat aus der Zufluss/Abgaben Funktion zu beeinflussen, was insbesondere bei geringen Speicherfüllungen wünschenswert ist.
- Schließlich muss die geforderte Abgabe noch hinsichtlich der Leistungskapazität der Auslassorgane überprüft werden.
- Nachfolgend sind Beispiele aufgeführt, wie sich das Zusammenspiel verschiedener Funktionen bezüglich der Abgaben auswirkt. Die Ergebnisse sind in den folgenden Abbildungen in Form von Zufluss- und Abgabendauerlinien gegenübergestellt.
- Bei linearem Zusammenhang zwischen Zufluss und Abgabe und konstantem Faktor über den Speicherinhalt ist die Dauerlinie der Abgabe eine in ihrer Form dem Zufluss entsprechende aber um einen bestimmten Prozentsatz reduzierte Kurve. Bei gleich bleibender Faktor/Speicherinhalts Beziehung kann durch Variation in der Zufluss/Abgaben Beziehung die Dauerlinie gezielt verändert werden. Eine zusätzliche Modifikation des Faktors über den Speicherinhalt bringt den Vorteil, auf bestimmte Füllungszustände reagieren zu können, um einem Leer- oder Überlaufen des Speichers entgegenzuwirken.
Regel Typ 7: Beeinflussung einer Abgabe durch Systemzustände
- Abhängigkeit:
- Die Regel 7 ist eine Weiterführung und Verallgemeinerung der Niedrigwasseraufhöhung wie in Regel 5 geschildert. Auch die Regel 6 fällt unter diese Rubrik. Genauso wie ein Abflussdefizit an einem Gewässerquerschnitt oder der Speicherzufluss eine Abgabe beeinflussen kann, können auch beliebige andere Systemzustände auf die zu tätigenden Abgaben einwirken. Allgemein formuliert bedeutet dies, dass eine Abgabe aus einem Speicher aufgrund eines bestimmten Systemzustandes ausgelöst, erhöht oder reduziert wird. Grundsätzlich ist es dabei unerheblich, an welchem Ort der Systemzustand auftritt. Als Systemzustände kommen prinzipiell alle messbaren, auf Transport und Speicherung von Wasser Einfluss nehmende Größen in Frage, wie z.B. Füllungen anderer Speicher, Abgaben, Abfluss an einem Gewässerquerschnitt, eine Schneehöhe im Einzugsgebiet, aktueller Niederschlag, aktuelle Bodenfeuchte, usw..
- Voraussetzung für die Anwendung solcher Abhängigkeiten ist die Erfassung des Systemzustandes. Praktisch bedeutet das, es muss eine Messeinrichtung zur Ermittlung der Größe vorhanden sein oder der erforderliche Wert wird über ein mathematisches Modell berechnet. Betrachtet werden ausschließlich momentane Größen.
- Sollen mehrere Systemzustände Einfluss auf die Abgabe nehmen, ist eine Überlagerung der Zustandsgrößen gemäß einer entsprechenden Vorschrift notwendig.
- Mathematische Abstraktion:
- Mathematisch lässt sich die Beeinflussung der Abgabe durch Systemzustände immer mit einer Skalierung lösen. Dazu sind zwei Funktionen notwendig. Die erste Funktion beschreibt die Beziehung zwischen Speicherinhalt und Abgabe. Die zweite regelt die Abhängigkeit zwischen Systemzustand und einem Skalierungsfaktor. Die Verknüpfung erfolgt durch Multiplikation der Abgabe mit dem Skalierungsfaktor.
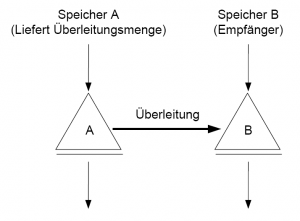
- Ein einfaches Beispiel ist durch eine Überleitung von Speicher A nach Speicher B gegeben.
- Die maßgebende Abgabe ist die Überleitung von A nach B. Der betrachtete Systemzustand ist der Speicherinhalt von B. Es erscheint sofort einsichtig, dass eine Wasserabgabe von A nach B nur dann sinnvoll ist, wenn Speicher A genügend Reserven zur Verfügung hat und Speicher B ausreichend Aufnahmekapazität für zusätzliches Wasser besitzt. Damit ergeben sich folgende einfachen Funktionen:
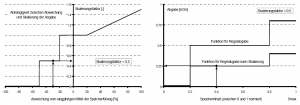
- Speicher B nimmt 100% des Zuschusses von A auf, solange seine Füllung nicht 70% des maximalen Inhaltes erreicht. Darüber hinaus ist es aus Gründen des Hochwasserschutzes unerwünscht, zusätzliches Wasser zu erhalten. Der Skalierungsfaktor fällt ab 70% Füllung bis auf Null ab. Speicher A kann ab einem Füllungsgrad über 50% Wasser an B mit steigender Tendenz überleiten. Die tatsächliche Überleitung ergibt sich aber erst im Zusammenspiel beider Funktionen unter Berücksichtigung der momentanen Speicherfüllung von B und der daraus abgeleiteten Skalierung.
- Für Speicher A erfolgt die Definition der Abgaben in m³/s, während die Funktion am Speicher B den einheitenlosen Skalierungsfaktor erhält. Prinzipiell ist es aber genauso denkbar, die Bedeutung der Funktionen zu tauschen und für Speicher A eine einheitenlose Funktion zur Skalierung der gewünschten Überleitungsmenge bei Speicher B einzusetzen.
Regel Typ 8: Beeinflussung einer Abgabe durch Bilanzen
- Abhängigkeit:
- Diese Vorschrift ist eine Erweiterung der Regel Nr. 7. Anstatt eine aktuelle Zustandsgröße zu benutzen, wird die Bilanz eines Systemzustandes mit einer Abgabe verknüpft. Wichtig ist, dass für die Bildung der Bilanz ein eindeutiger Zeitraum vorliegt, wobei es unerheblich ist, ob die Bilanz als Summe oder als Mittelwert interpretiert wird. Über eine Funktion, die Skalierungsfaktoren in Abhängigkeit der tatsächlichen Bilanz anzeigt, lassen sich Abgaben beeinflussen.
- In der Praxis findet sich diese Form einer Abhängigkeit häufig dort wo Wasserrechte maximale Entnahmemengen je Zeiteinheit festlegen. Interessant ist die Anwendung einer Bilanz aber auch im Zusammenhang mit dem langfristigen Verhalten von Speicherfüllungen oder Zuflüssen. So könnte z.B. zur Bildung von Reserven eine Abgabe reduziert werden, wenn der Zufluss des vergangenen Winterhalbjahres unter einem definierten Erwartungswert lag. Eine weitere Anwendung ist der Vergleich zwischen langjährigen und aktuellen gleitenden Mittelwerten der Speicherfüllung. Weichen die aktuellen Werte von den langjährigen um ein bestimmtes Maß ab, kann die Abgabe zum Ausgleich verringert bzw. erhöht werden.
- Sind mehrere Verknüpfungen zwischen einer Abgabe und verschiedenen Bilanzen erwünscht, besteht die Möglichkeit der Überlagerung mehrerer Bilanzen (siehe Beispiel am Ende dieses Kapitels).
- Mathematische Abstraktion:
- Der Einfluss der Bilanz auf die Abgabe wird mittels zweier Funktionen analog Regel 7 gebildet. Zusätzlich zur ohnehin notwendigen Speicherinhalt/Abgaben Funktion existiert eine Beziehung zwischen Bilanz und Skalierungsfaktor. Mit der Abweichung zwischen tatsächlicher Bilanz und Erwartungswert wird der Skalierungsfaktor abgegriffen.
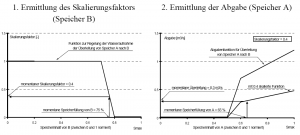
- Anhand eines einfachen Beispiels einer Regelabgabe wird die Methode demonstriert.
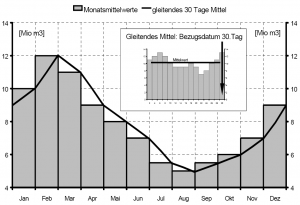
- Für einen Speicher A seien langjährige Monatsmittelwerte des Inhaltes und daraus abgeleitete gleitende 30 Tage Mittelwerte der Speicherfüllung sowie die Vorschrift für die Regelabgabe bekannt.
- Wenn beispielsweise am 1.Mai der aus den letzten 30 Tagen berechnete Mittelwert des Speicherinhaltes 5,6 Mio. m³ betragen würde und damit gemäß Abbildung 15 gegenüber dem langjährigen Mittelwert von 8 Mio. m³ um 30% abweicht, folgt daraus ein Skalierungsfaktor von 0,5 (siehe Abbildung 16). Mit diesem Wert reduziert sich die Regelabgabe und liefert bei einer aktuellen Speicherfüllung von 40% nur 0,25m³/s, also 50% weniger als vorgesehen.
- Die Beziehung zwischen Bilanzabweichung und Skalierungsfaktor zeigt an, dass erst ab einer Differenz größer als 20% eine Änderung der Regelabgabe stattfindet. Bei einer Abweichung von mehr als 20% nach unten reduziert sich die Regelabgabe stufenweise. Überschreitet das tatsächliche gleitende 30-Tage-Mittel die langjährigen Werte um mehr als 20%, so wird die Regelabgabe kontinuierlich erhöht.
- Grundsätzlich besteht auch hier die Möglichkeit der Erweiterung durch Überlagerung und Zusammenfassung mehrerer Bilanzen.
- Das Zusammenspiel zwischen Bilanz und Abgabenfunktion wird nachfolgend erläutert.
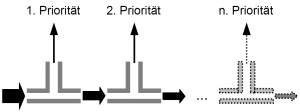
Regel Typ 9: Prioritäten bei mehreren, konkurrierenden Abgaben aus einem Speicher
- Abhängigkeit:
- Sind mehrere Abgaben aus einem Speicher zu tätigen, so kann die Situation eintreten, dass nicht alle Abgaben (Nutzungen) zu 100% erfüllt werden können. In solchen Fällen sind Prioritäten anzugeben, die eine Reihenfolge der zuerst zu befriedigenden Abgaben festlegen. Die Angabe der Prioritäten ist oftmals eine Folge politischer Entscheidungen und unterliegt keinen physikalischen Gegebenheiten.
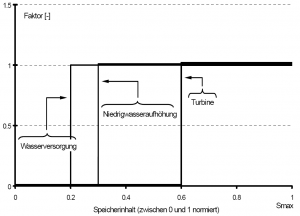
- Auf der anderen Seite existieren Prioritäten die sich an physikalischen Werten orientieren. Ein Beispiel in diesem Sinne ist das Abschalten einer Turbine in Zeiten des Wassermangels zugunsten einer gesicherten Wasserversorgung. In der Praxis benutzte Betriebsregeln begegnen diesem Problem häufig dadurch, dass bis zu definierten Speicherinhalten eine Nutzung erfüllt, darunter aber nicht mehr aufrechterhalten wird.
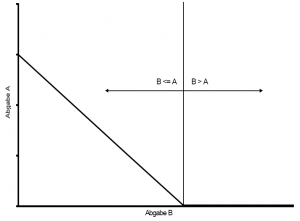
- Eine andere Form, Prioritäten zu beschreiben, ist gegeben, wenn eine Abgabe A genau um den Betrag reduziert wird, der durch eine zweite Abgabe B erfolgt, wobei die Abgabe A nicht kleiner Null werden kann.
- Praktisches Beispiel:
- Anhand der praktischen Betriebsverhältnisse an der Wiehltalsperre lässt sich ein solches Beispiel zeigen. Die Wiehltalsperre dient primär der Trinkwasserversorgung und dem Hochwasserschutz, sekundär der Energieerzeugung. Zusätzlich ist im Unterlauf der Wiehltalsperre ein Mindestabfluss von 100 l/s zu gewährleisten. Die erste Priorität gehört der Trinkwasserversorgung. Zur Sicherstellung einer ausreichenden Wasserqualität im Speicherbecken werden zur Energieerzeugung genutzte zusätzliche Abgaben dann eingestellt, wenn der Speicherinhalt unter ca. 70% des Gesamtinhaltes fällt. Da sowohl die Mindestabgabe als auch die Turbinenabgabe in die Wiehl abgelassen werden, wäre es außerdem überflüssig, die Mindestabgabe aufrecht zu erhalten, wenn gleichzeitig durch die Turbine Wasser abgegeben wird. Somit ergibt sich hier ein Fall der Reduzierung einer Abgabe A (Mindestabgabe) um den Betrag der Abgabe B (Turbine) wie oben beschrieben[2].
- Mathematische Abstraktion:
- Unter der Annahme, dass für jede Nutzung, wie unter den vorgenannten Regeln beschrieben, eine funktionale Abhängigkeit zwischen Speicherinhalt und Abgabe existiert, ist eine Rangfolge mehrerer Nutzungen durch die Lage der Stützstellen der Funktionen bereits gegeben. Entscheidend ist der jeweilige Speicherinhalt ab dem der Sollwert der gewünschten Abgabe nicht mehr zu 100% gedeckt wird oder sogar eine Reduzierung auf Null erfolgt.
- Im gezeigten Beispiel ist die Rangfolge der Nutzungen eindeutig sichtbar. Zuerst wird die Turbine, danach die Niedrigwasseraufhöhung abgeschaltet bis nur noch die Abgabe für die Wasserversorgung übrig bleibt.
- Darüber hinaus besteht die Möglichkeit, zwei oder mehrere Abgaben direkt gegenseitig abzugleichen. Eine solche Vorschrift könnte lauten:
- Wenn Abgabe B > 0 und der Speicherinhalt S < X, dann reduziere Abgabe A um den Betrag der Abgabe B, wobei Abgabe A nicht kleiner als Null werden darf.
- Das bedeutet, dass zwischen A und B eine lineare Abhängigkeit solange existiert, bis B gleich dem Wert von A ist. Steigt B weiter an, bleibt A konstant Null.
Regel Typ 11: Wasseraufteilung
- Abhängigkeit:
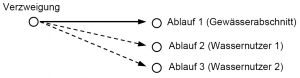
- Existiert innerhalb eines wasserwirtschaftlichen Systems die Notwendigkeit Wasser aufzuteilen, so ist eine Verteilungsvorschrift zu definieren.
- Es können zwei Arten von Aufteilungen auftreten:
- Aufteilungen, die ausschließlich hydraulischen Gesetzmäßigkeiten folgen
- Regelbare Aufteilungen
- In beiden Fällen lassen sich Beziehungen immer als Funktion des Zuflusses definieren. Im zweiten Fall stellen diese Aufteilungsvorschriften eine Betriebsregel dar, da sie direkt das Transport- und Speicherverhalten des Wassers beeinflussen. Die Anzahl der abgehenden Abläufe ist grundsätzlich nicht eingeschränkt. Der Unterschied zu Aufteilungen an Talsperren liegt darin, dass in diesem Fall kein Speicherinhalt als Bezugsgröße Verwendung finden kann.
- Praktisches Beispiel:
- Zur Wasserversorgung von Windhoek, der Hauptstadt Namibias, stehen die Wasserreserven dreier Dämme zur Verfügung. Die Entnahme zur Trinkwasserversorgung ist jedoch nur aus einem Damm – Von Bach Damm - möglich. Die restlichen zwei Speicher sind mit Überleitungen an den Hauptdamm angeschlossen. Die Überleitungsmenge zwischen Swakopport Damm und Von Bach Damm steht aber nicht ausschließlich für die Auffüllung des Von Bach Dammes zur Verfügung, sondern dient außerdem für die Versorgung der Stadt Karibib mit Trinkwasser.
- Mathematische Abstraktion:
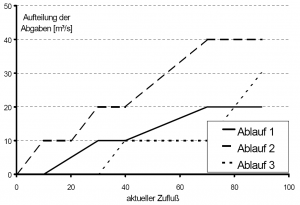
- Für die Definition von Aufteilungsvorschriften sind Funktionen in Abhängigkeit des aktuellen Zuflusses die geeignete Darstellung. Damit gelingt sowohl eine hydraulische als auch eine der Speicherbewirtschaftung dienende Beschreibung. Für jeden vom Verzweigungsbauwerk abgehenden Ablauf ist eine Zuteilungsfunktion anzugeben. Sollen die Funktionen variabel sein, bietet sich wiederum eine Skalierung an.
- Sind die Zuteilungsfunktionen nicht a priori definierbar, sondern ergeben sich die abzuleitenden Mengen erst später durch Bedarfsberechnungen, so bietet sich ein Schwellwertkonzept an, welches wiederum mit Skalierungsfaktoren arbeiten kann. Der Schwellwert wird über einen Faktor skaliert und ist dadurch variabel. Solange der Zufluss geringer als der Schwellwert ist, wird der gesamte Zufluss zur Befriedigung des Bedarfs benutzt. Erst wenn der aktuelle Zufluss den Schwellwert übersteigt, kommt es zum Abschlag der restlichen Menge.
- Ist eine Aufteilung in mehr als zwei Abläufe notwendig, kann das Schwellwertkonzept mehrfach nacheinander angewandt werden. Die Reihenfolge entscheidet über die Prioritäten der Wasserzuteilung.
Literaturangaben
- ↑ Schultz, G.A. (1989): Entwicklung von Betriebsregeln für die Wupper-Talsperre in Niedrig- und Hochwasserzeiten. Wasserwirtschaft 79 (7/8) S. 340-343
- ↑ Aggerverband (1999): Hydrologische Sicherheit der Genkel- und Aggertalsperre. Gutachten des Fachgebietes Ingenieurhydrologie und Wasserbewirtschaftung, TU Darmstadt