Berechnungsschema/ Implementierung der Betriebsregeln/en: Unterschied zwischen den Versionen
Ferrao (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „For a section of the function applies:“) |
Keine Bearbeitungszusammenfassung |
||
| (68 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
{{Navigation|vorher=Abstraktion der Betriebsregeln|hoch=Betriebsregelkonzept|nachher=Anwendungsbeispiel: Umsetzung eines Betriebsplans}} | {{Navigation|vorher=Abstraktion der Betriebsregeln|hoch=Betriebsregelkonzept|nachher=Anwendungsbeispiel: Umsetzung eines Betriebsplans}} | ||
To operationalize principles for simulation, it is required to devise mathematical relations. | |||
The order of | The previously given order of principles already indicates a useful structure for the mathematical formulation. The storage volume poses the most essential dependency. In system hydrology, this type of dependency is known as a linear single stroage and can be thoroughly solved. Its principle is based on the assumption that the discharge is always proportional to the amount of water present in the storage (storage volume). The proportionality factor k is referred to as the storage constant. Taking into account the continuity equation and the storage constant gives the differential equation of the linear single storage. However, the storage equation is inapplicable to storage systems influenced by controls and operation rules. In this case, the discharges are not proportional to the storage volume, and therefore, an extension of the equation to any number of discharges is necessary. | ||
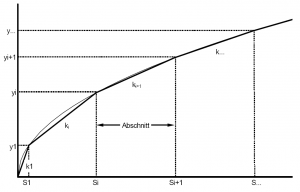
[[Bild:Theorie_Abb24.png|thumb| | [[Bild:Theorie_Abb24.png|thumb|Figure 24: Linearization of a function - section by section ]] | ||
Operation rules and controls need to be implemented to the set of equations by considering the relation of the storage volume to the discharge. As exemplarily shown in this chapter, this relation is usually only available in the form of supporting points. Linearly connecting supporting points leads to a characteristic curve. Here, the connection of supporting points results in a discharge function. A general demonstration of the linearization process, section by section, is given in [[:Bild:Theorie_Abb24.png|Figure 24]]. | |||
One section can be described by: | |||
<div style="float:right">(2-1)</div> | <div style="float:right">(2-1)</div> | ||
:<math>y_{(t)}=y_{i-1}+k_i \cdot (S_{(t)} - S_{i-1})</math> | :<math>y_{(t)}=y_{i-1}+k_i \cdot (S_{(t)} - S_{i-1})</math> | ||
: | :with | ||
:<math>S_i < S_{(t)} \le S_{i+1}</math> | :<math>S_i < S_{(t)} \le S_{i+1}</math> | ||
For any number of discharge functions, the equation of a linear single storage for a section is: | |||
<div style="float:right">(2-2)</div> | <div style="float:right">(2-2)</div> | ||
:<math>\frac{dS}{dt} = \sum_{z=1}^n Q_z - \sum_{p=1}^m (y_{p,i-1} + k_{p,i} \cdot (S_{(t)} - S_{p,i-1}))</math> | :<math>\frac{dS}{dt} = \sum_{z=1}^n Q_z - \sum_{p=1}^m (y_{p,i-1} + k_{p,i} \cdot (S_{(t)} - S_{p,i-1}))</math> | ||
: | :with | ||
:S : | :S : Storage volume | ||
:Q<sub>z</sub> : | :Q<sub>z</sub> : Inflow (independent of storage volume). | ||
:y<sub>i-1</sub> : | :y<sub>i-1</sub> : Discharge value at supporting point i-1 | ||
:k : | :k : Slope between the supporting points i-1 and i | ||
:n : | :n : Number of inflows | ||
:m : | :m : Number of discharges dependent on the storage volume | ||
:t : | :t : Time | ||
After dividing the equation into a constant part and a part depending on the storage volume S, the known and solvable equation of the linear single storage is obtained. | |||
<div style="float:right">(2-3)</div> | <div style="float:right">(2-3)</div> | ||
:<math>\frac{dS}{dt} = \begin{matrix} \underbrace {\sum_{z=1}^n Q_z - \sum_{p-1}^m ( y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} )} \\ C_1=\mbox{ | :<math>\frac{dS}{dt} = \begin{matrix} \underbrace {\sum_{z=1}^n Q_z - \sum_{p-1}^m ( y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} )} \\ C_1=\mbox{constant part} \end{matrix} - \begin{matrix} \underbrace {\sum_{p=1}^m (k_{p,i})} \\ C_2=\mbox{depending on S} \end{matrix} \cdot S_{(t)}</math> | ||
:<math>\frac{dS}{dt} = C_1 - C_2 \cdot S_{(t)} </math> | :<math>\frac{dS}{dt} = C_1 - C_2 \cdot S_{(t)} </math> | ||
As long as the storage volumes are within one section <code>S<sub>i-1</sub></code> to <code>S<sub>i</sub></code>, the solution to the differential equation is: | |||
<div style="float:right">(2-4)</div> | <div style="float:right">(2-4)</div> | ||
:<math>S(t) = \frac{C_1}{C_2} \cdot \left [ 1 - e^{-C_2} \cdot (t-t_0) \right ]</math> | :<math>S(t) = \frac{C_1}{C_2} \cdot \left [ 1 - e^{-C_2} \cdot (t-t_0) \right ]</math> | ||
If at least one discharge function exceeds the viewed section, respective changes to the storage volumes and to the discharges must be identified up to that point and <code>C<sub>1</sub></code> and <code>C<sub>2</sub></code> recalculated. With this method, the used time interval - the outer time step - is processed by an arbitrary number of inner time steps, depending on the closeness of the supporting points. The time it takes to undertake a section change can be determined by solving the following equation for <code>t</code>: | |||
<div style="float:right">(2-5)</div> | <div style="float:right">(2-5)</div> | ||
:<math>t_1 = -\frac{1}{C_2} \cdot \ln \left ( \frac{S(t)-\frac{C_1}{C_2}}{S_0-\frac{C_1}{C_2}} \right ) + t_0</math> | :<math>t_1 = -\frac{1}{C_2} \cdot \ln \left ( \frac{S(t)-\frac{C_1}{C_2}}{S_0-\frac{C_1}{C_2}} \right ) + t_0</math> | ||
Whether a storage volume increases or decreases within the viewed section is to be determined by substituting <code>S(t)</code> by the upper section boundary, whereupon the nearest supporting point of all functions is crucial for the determination of the section boundary. The resulting value <code>t<sub>1</sub></code> determines the following three cases: | |||
# <math>t_1 > \Delta t \,</math> ( | # <math>t_1 > \Delta t \,</math> (outer time step) | ||
#: | #: In the considered time interval, no section change takes place . | ||
# <math>0 < t_1 < \Delta t \,</math> | # <math>0 < t_1 < \Delta t \,</math> | ||
#: | #: After the time <code>t<sub>1</sub></code>, there is a section change . The span between <code>t<sub>0</sub></code> and <code>t<sub>1</sub></code> represents the length of the inner time step. | ||
# <math>t_1 < 0 \,</math> | # <math>t_1 < 0 \,</math> | ||
#: | #: There is no storage content increase but a decrease. Instead of the upper section boundary, the lower section boundary must be used and the calculation repeated. | ||
If section changes are observed, the storage volume is known at every time <code>t</code>. Consequently, processes depending on the storage volumes are also known. In general, the development of the curve over time is not required but rather the mean value within one time interval. If equation 2-4 is inserted into equation 2-1 and integrated over the inner time step length, the average process rate in the relevant time interval is obtained. | |||
<div style="float:right">(2-6)</div> | <div style="float:right">(2-6)</div> | ||
:<math>\bar{y} = y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + k_{p,i} \cdot \left [ \frac{C_1}{C_2} + \left ( 1-e^{-C_2} \cdot (t_1-t_0) \right ) \cdot \left ( \frac{S_0}{(t_1-t_0) \cdot C_2} - \frac{C_1}{(t_1-t_0) \cdot C_2^2} \right ) \right ] </math> | :<math>\bar{y} = y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + k_{p,i} \cdot \left [ \frac{C_1}{C_2} + \left ( 1-e^{-C_2} \cdot (t_1-t_0) \right ) \cdot \left ( \frac{S_0}{(t_1-t_0) \cdot C_2} - \frac{C_1}{(t_1-t_0) \cdot C_2^2} \right ) \right ] </math> | ||
After summing up the inner time step values, the average process rate over the entire outer time interval is obtained. | |||
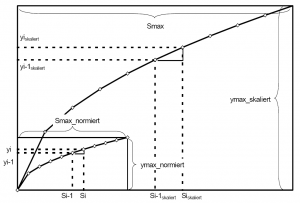
[[Bild:Theorie_Abb25.png|thumb| | [[Bild:Theorie_Abb25.png|thumb|Figure 25: Linearization of a scaled discharge function - section by section]] | ||
The principles in the description of operating rules illustrate that discharges depend on storage volumes as well as on other system states. Thus, a one-dimensional dependency no longer exists but rather a two- or multi-dimensional relation. Considering also a time dependency the problem is extended by one more dimension. Therefore, the solution from above, and respectively a simple depiction in a diagram, are no longer possible. For clarity and adequate mathematical formulation, a conversion from multiple dependencies to a one-dimensional relation needs to be undertaken without a loss of information. Scaling the discharge functions relation achieves said conversion. It is possible for the discharge (y-axis) as well as for the storage volumes (x-axis). | |||
After introducing the scaling factors, the result for a scaled section of a function is: | |||
<div style="float:right">(2-7)</div> | <div style="float:right">(2-7)</div> | ||
:<math>y_{(t)}^s = y_{i-1} \cdot y_{\mbox{ | :<math>y_{(t)}^s = y_{i-1} \cdot y_{\mbox{factor}} + k_i \cdot \frac{y_{\mbox{factor}}}{x_{\mbox{factor}}} \cdot \left ( S_{(t)} \cdot x_{\mbox{factor}} -S_{i-1} \cdot x_{\mbox{factor}} \right )</math> | ||
:<math>y_{(t)}^s = y_{i-1}^s + k_i^s \cdot \left ( S_{(t)}^s - S_{i-1}^s \right )</math> | :<math>y_{(t)}^s = y_{i-1}^s + k_i^s \cdot \left ( S_{(t)}^s - S_{i-1}^s \right )</math> | ||
To calculate the delivery function scaled with external system states, proceed analogously to the above method. Here, <code>x<sub>factor</sub></code> corresponds to the maximum storage volume and <code>y<sub>factor</sub></code> corresponds to the scaling factor from the external system state or state group. It is assumed that the factors remain constant during the outer time interval. The sum of the integrations over the internal time loop divided by the outer time step provides the final output value. | |||
<div style="float:right">(2-8)</div> | <div style="float:right">(2-8)</div> | ||
:<math>\bar{y} = y_{\mbox{faktor}} \cdot \left [ y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + \frac{1}{x_{\mbox{faktor}}} k_{p,i} \cdot \left [ \frac{\mbox{C1}^s}{\mbox{C2}^s} + \left ( 1 - \mbox{e}^{-\mbox{C2}^s \cdot \left ( t_1 - t_0 \right )} \right ) \cdot \left ( \frac{S_0 \cdot x_{\mbox{faktor}}}{(t_1 - t_0) \cdot \mbox{C2}^s} - \frac{\mbox{C1}^s}{(t_1 - t_0) \cdot {\mbox{C2}^s}^2} \right ) \right ] \right ]</math> | :<math>\bar{y} = y_{\mbox{faktor}} \cdot \left [ y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + \frac{1}{x_{\mbox{faktor}}} k_{p,i} \cdot \left [ \frac{\mbox{C1}^s}{\mbox{C2}^s} + \left ( 1 - \mbox{e}^{-\mbox{C2}^s \cdot \left ( t_1 - t_0 \right )} \right ) \cdot \left ( \frac{S_0 \cdot x_{\mbox{faktor}}}{(t_1 - t_0) \cdot \mbox{C2}^s} - \frac{\mbox{C1}^s}{(t_1 - t_0) \cdot {\mbox{C2}^s}^2} \right ) \right ] \right ]</math> | ||
The computation of a section-by-section linear memory with arbitrary many inputs and outputs has been described by Ostrowski (1992)<ref name="Ostrowski_1992">'''Ostrowski, M.''' (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11</ref>. This solution was extended to include scaling of both the x-axis and y-axis by Ostrowski (1999)<ref name="Ostrowski_1999">'''Ostrowski, M. et al.''' (1999): Ein universeller, nicht linearer Speicherbaustein zur Simulation hydrologischer Systeme. Institutseigene Modell- und Anwendungsbeschreibung, Institut für Wasserbau und Wasserwirtschaft, TU Darmstadt, unveröffentlicht</ref>. | |||
In summary, a storage can have multiple uses. For each use, there is a function depending on the storage volume, which must remain constant within an outer time step, but is changeable from time step to time step (time dependency). Besides, scaling the functions differently for each time step accounts for external dependencies via factors. Prerequisites for the scaling are constant factors during the time step. The calculation process is independent of the time step, as it is split according to section changes into an arbitrary number of inner time steps. As a result, the method is suitable for a wide variety of time intervals and produces results that are true to the volume. The method facilitates its use for diverse time intervals, e.g. it is suitable for a flood event with a time step of a few minutes but as well for a long-term simulation with daily values or even larger time intervals. For this purpose, it is critical, to define discharge functions with a sufficient number of supporting points. | |||
== | ==Literature references== | ||
<references/> | <references/> | ||
Aktuelle Version vom 30. August 2021, 10:27 Uhr
To operationalize principles for simulation, it is required to devise mathematical relations.
The previously given order of principles already indicates a useful structure for the mathematical formulation. The storage volume poses the most essential dependency. In system hydrology, this type of dependency is known as a linear single stroage and can be thoroughly solved. Its principle is based on the assumption that the discharge is always proportional to the amount of water present in the storage (storage volume). The proportionality factor k is referred to as the storage constant. Taking into account the continuity equation and the storage constant gives the differential equation of the linear single storage. However, the storage equation is inapplicable to storage systems influenced by controls and operation rules. In this case, the discharges are not proportional to the storage volume, and therefore, an extension of the equation to any number of discharges is necessary.
Operation rules and controls need to be implemented to the set of equations by considering the relation of the storage volume to the discharge. As exemplarily shown in this chapter, this relation is usually only available in the form of supporting points. Linearly connecting supporting points leads to a characteristic curve. Here, the connection of supporting points results in a discharge function. A general demonstration of the linearization process, section by section, is given in Figure 24.
One section can be described by:
- [math]\displaystyle{ y_{(t)}=y_{i-1}+k_i \cdot (S_{(t)} - S_{i-1}) }[/math]
- with
- [math]\displaystyle{ S_i \lt S_{(t)} \le S_{i+1} }[/math]
For any number of discharge functions, the equation of a linear single storage for a section is:
- [math]\displaystyle{ \frac{dS}{dt} = \sum_{z=1}^n Q_z - \sum_{p=1}^m (y_{p,i-1} + k_{p,i} \cdot (S_{(t)} - S_{p,i-1})) }[/math]
- with
- S : Storage volume
- Qz : Inflow (independent of storage volume).
- yi-1 : Discharge value at supporting point i-1
- k : Slope between the supporting points i-1 and i
- n : Number of inflows
- m : Number of discharges dependent on the storage volume
- t : Time
After dividing the equation into a constant part and a part depending on the storage volume S, the known and solvable equation of the linear single storage is obtained.
- [math]\displaystyle{ \frac{dS}{dt} = \begin{matrix} \underbrace {\sum_{z=1}^n Q_z - \sum_{p-1}^m ( y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} )} \\ C_1=\mbox{constant part} \end{matrix} - \begin{matrix} \underbrace {\sum_{p=1}^m (k_{p,i})} \\ C_2=\mbox{depending on S} \end{matrix} \cdot S_{(t)} }[/math]
- [math]\displaystyle{ \frac{dS}{dt} = C_1 - C_2 \cdot S_{(t)} }[/math]
As long as the storage volumes are within one section Si-1 to Si, the solution to the differential equation is:
- [math]\displaystyle{ S(t) = \frac{C_1}{C_2} \cdot \left [ 1 - e^{-C_2} \cdot (t-t_0) \right ] }[/math]
If at least one discharge function exceeds the viewed section, respective changes to the storage volumes and to the discharges must be identified up to that point and C1 and C2 recalculated. With this method, the used time interval - the outer time step - is processed by an arbitrary number of inner time steps, depending on the closeness of the supporting points. The time it takes to undertake a section change can be determined by solving the following equation for t:
- [math]\displaystyle{ t_1 = -\frac{1}{C_2} \cdot \ln \left ( \frac{S(t)-\frac{C_1}{C_2}}{S_0-\frac{C_1}{C_2}} \right ) + t_0 }[/math]
Whether a storage volume increases or decreases within the viewed section is to be determined by substituting S(t) by the upper section boundary, whereupon the nearest supporting point of all functions is crucial for the determination of the section boundary. The resulting value t1 determines the following three cases:
- [math]\displaystyle{ t_1 \gt \Delta t \, }[/math] (outer time step)
- In the considered time interval, no section change takes place .
- [math]\displaystyle{ 0 \lt t_1 \lt \Delta t \, }[/math]
- After the time
t1, there is a section change . The span betweent0andt1represents the length of the inner time step.
- After the time
- [math]\displaystyle{ t_1 \lt 0 \, }[/math]
- There is no storage content increase but a decrease. Instead of the upper section boundary, the lower section boundary must be used and the calculation repeated.
If section changes are observed, the storage volume is known at every time t. Consequently, processes depending on the storage volumes are also known. In general, the development of the curve over time is not required but rather the mean value within one time interval. If equation 2-4 is inserted into equation 2-1 and integrated over the inner time step length, the average process rate in the relevant time interval is obtained.
- [math]\displaystyle{ \bar{y} = y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + k_{p,i} \cdot \left [ \frac{C_1}{C_2} + \left ( 1-e^{-C_2} \cdot (t_1-t_0) \right ) \cdot \left ( \frac{S_0}{(t_1-t_0) \cdot C_2} - \frac{C_1}{(t_1-t_0) \cdot C_2^2} \right ) \right ] }[/math]
After summing up the inner time step values, the average process rate over the entire outer time interval is obtained.
The principles in the description of operating rules illustrate that discharges depend on storage volumes as well as on other system states. Thus, a one-dimensional dependency no longer exists but rather a two- or multi-dimensional relation. Considering also a time dependency the problem is extended by one more dimension. Therefore, the solution from above, and respectively a simple depiction in a diagram, are no longer possible. For clarity and adequate mathematical formulation, a conversion from multiple dependencies to a one-dimensional relation needs to be undertaken without a loss of information. Scaling the discharge functions relation achieves said conversion. It is possible for the discharge (y-axis) as well as for the storage volumes (x-axis).
After introducing the scaling factors, the result for a scaled section of a function is:
- [math]\displaystyle{ y_{(t)}^s = y_{i-1} \cdot y_{\mbox{factor}} + k_i \cdot \frac{y_{\mbox{factor}}}{x_{\mbox{factor}}} \cdot \left ( S_{(t)} \cdot x_{\mbox{factor}} -S_{i-1} \cdot x_{\mbox{factor}} \right ) }[/math]
- [math]\displaystyle{ y_{(t)}^s = y_{i-1}^s + k_i^s \cdot \left ( S_{(t)}^s - S_{i-1}^s \right ) }[/math]
To calculate the delivery function scaled with external system states, proceed analogously to the above method. Here, xfactor corresponds to the maximum storage volume and yfactor corresponds to the scaling factor from the external system state or state group. It is assumed that the factors remain constant during the outer time interval. The sum of the integrations over the internal time loop divided by the outer time step provides the final output value.
- [math]\displaystyle{ \bar{y} = y_{\mbox{faktor}} \cdot \left [ y_{p,i-1} - k_{p,i} \cdot S_{p,i-1} + \frac{1}{x_{\mbox{faktor}}} k_{p,i} \cdot \left [ \frac{\mbox{C1}^s}{\mbox{C2}^s} + \left ( 1 - \mbox{e}^{-\mbox{C2}^s \cdot \left ( t_1 - t_0 \right )} \right ) \cdot \left ( \frac{S_0 \cdot x_{\mbox{faktor}}}{(t_1 - t_0) \cdot \mbox{C2}^s} - \frac{\mbox{C1}^s}{(t_1 - t_0) \cdot {\mbox{C2}^s}^2} \right ) \right ] \right ] }[/math]
The computation of a section-by-section linear memory with arbitrary many inputs and outputs has been described by Ostrowski (1992)[1]. This solution was extended to include scaling of both the x-axis and y-axis by Ostrowski (1999)[2].
In summary, a storage can have multiple uses. For each use, there is a function depending on the storage volume, which must remain constant within an outer time step, but is changeable from time step to time step (time dependency). Besides, scaling the functions differently for each time step accounts for external dependencies via factors. Prerequisites for the scaling are constant factors during the time step. The calculation process is independent of the time step, as it is split according to section changes into an arbitrary number of inner time steps. As a result, the method is suitable for a wide variety of time intervals and produces results that are true to the volume. The method facilitates its use for diverse time intervals, e.g. it is suitable for a flood event with a time step of a few minutes but as well for a long-term simulation with daily values or even larger time intervals. For this purpose, it is critical, to define discharge functions with a sufficient number of supporting points.
Literature references
- ↑ Ostrowski, M. (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11
- ↑ Ostrowski, M. et al. (1999): Ein universeller, nicht linearer Speicherbaustein zur Simulation hydrologischer Systeme. Institutseigene Modell- und Anwendungsbeschreibung, Institut für Wasserbau und Wasserwirtschaft, TU Darmstadt, unveröffentlicht