Betriebsplan
Talsim-NG schließt ein Bewirtschaftungsmodell mit ein, d.h. es bietet die Möglichkeit Speicher und Aufteilungsbauwerke mittels konkreter Vorschriften zu regeln. Die in Realität bestehenden oder geplanten Betriebsregeln müssen dazu in eine Form gebracht werden, mit der Talsim-NG rechnet kann.
Was in der Realität Messungen im Flussgebiet sind, kann in Talsim-NG durch das Abgreifen von sogenannten Systemzuständen der Systemelementen abgebildet werden. Diese Systemzustände können weiterverarbeitet werden und mittels mathematischer und logischer Operatoren zu Zustandsgruppen verknüpft werden (auch mehrfach hintereinander). Aufgrund der Vielfalt der Optionen und Verknüpfungsmöglichkeiten, können beinahe beliebige Regeln abgebildet werden. Der Systemzustand/ die Zustandsgruppe, die so die letztendliche Betriebsregel repräsentiert, wird in dem Systemelement angeschlossen, das damit geregelt werden soll. Handelt es sich bei dem Systemelement um einen Speicher können dann gegebenenfalls noch physikalische Grenzen für die Abgabe, sowie die internen Abhängigkeiten zwischen verschiedenen Abgaben eingegeben werden. Somit erhält man die Steuerlogik für das Flussgebietsmodell.
Systemzustand
Um zu entscheiden, welcher Systemzustand/ welche Systemzustände für das Erstellen wie definiert werden sollen, ist es hilfreich sich für jede Betriebsregel folgende Fragen zu beantworten.
| Thema | Fragen zur realen Regel | Fragen zum Talsim-NG-Flussgebietsmodell | Umsetzung in Talsim-NG |
|---|---|---|---|
| Messgröße | Auf welchem Messwert/ welchen Messwerten beruhen die Regeln? Welcher Parameter wird gemessen? | Welcher Simulationsgröße entspricht das, bzw. aus welcher Simulationsgröße könnte der Parameter abgeleitet werden? Sämtliche Simulationsgrößen, d.h. Ein-, Ausgangs- und Zustandsgrößen der Systemelemente stehen prinzipiell zur Verfügung (z.B. Zufluss, Abfluss, Speicherinhalt, ...). | Konkretes Systemelement und Parameter auswählen → Systemzustand anlegen |
| Räumlicher Bezug | An welchem Ort wird gemessen? | Welches konkrete Systemelement (Kennung) kann also die Messung (mit welcher Simulationsgröße als Systemzustand) repräsentieren? | |
| Zeitlicher Bezug | Wie ist der zeitliche Bezug der Messung? Wird z.B. der aktuelle Wert verwendet, eine Bilanz oder Werte vom Vortag? | Mit welcher Option in Talsim-NG kann der zeitliche Bezug am Besten dargestellt werden? | Zweck des Systemzustandes festlegen und Optionen zur Werteänderung entsprechend einstellen |
| Transformation | Wird der Messwert nachträglich noch verändert, bevor er in die Betriebsregel eingeht (z.B. Umrechnung der Einheiten, Gewichtung,...)? | Mit welcher der Funktionen aus Talsim-NG kann die Transformation dargestellt werden? | Auswahl und Definition der Transformationsfunktion des Systemzustandes |
Nachdem die Fragen zu Ort der Messung und dem Parameter geklärt sind, kann der Systemzustand angelegt werden. Für diesen Systemzustand können dann die Zustandsattribute festgelegt werden. Dafür stehen folgende Optionen zur Verfügung:
Zustandsattribut Zweck
Talsim-NG bietet folgende Optionen den Typ oder auch Zweck des Systemzustandes festzulegen:
| A | Aktueller Wert | verwendet den aktuellen Wert ohne Veränderung |
| F | Funktion | Wert wird mittels einer Funktion transformiert |
| B | Bilanz (mit Zielwert) | Wert wird als Abweichung vom Soll in % verwendet |
| C | Bilanz (ohne Zielwert) | Wert wird über Zeitschritte bilanziert) |
| Z | Zielfunktion | Wert ist Ergebnis einer Zielfunktion |
| P | Unterwasserpegel | momentan deaktiviert |
| S | Summe | Summe des Zustandes anstatt Einzelwerte |
Aktueller Wert
Die Option aktueller Wert verwendet den im aktuellen Zeitschritt simulierten Wert ohne Veränderung:
Ergebnis = Aktueller Wert des Systemzustandes
Funktion
Die Option Funktion hat als zeitlichen Bezug ebenfalls den aktuellen Zeitschritt, allerdings schließt sie die Möglichkeit ein, den Wert mittels einer Funktion zu transformieren. Da auch die anderen Optionen (Ausnahme: aktueller Wert) anschließend transformiert werden können, wird das erst im nächsten Abschnitt erläutert.
Bilanz
Die Bilanz kann definiert werden als
- Mittelwert der letzten n Zeitschritte (max. 1200)
- Fixer Zeitraum (Startdatum bis Enddatum)
- Konstanter Zeitraum (gleitendes Mittel)
- i-ter Zeitschritt
Bei der Bilanz ohne Zielwert, ist die Bilanz selbst der Startwert für die anschließende Transformation.
Bei der Bilanz mit Zielwert geht die Abweichung als Startwert in die Transformation ein und diese wird wie folgt berechet:
Abweichung = ((BILANZ- Soll) / Soll) * 100
Der Sollwert wird dazu als Konstante ggfs. skaliert mit einem Jahresgang definiert.
Summe
Werteänderung
Transformationsfunktion
Die Systemzustände können zusätzlich noch über Funktionen transformiert werden (Ausnahme: Zweck aktueller Wert). Es gibt die Optionen
|
Kennlinie |
|
Konstanter Jahresgang |
|
Variabler Jahresgang |
|
Lamellenplan |
|
Zeitabhängige Funktion |
Kennlinie
Die einfachste Option und zugleich Voreinstellung für Systemzustände, die nicht als Aktueller Wert behandelt werden ist die der Kennlinie. Hierbei werden die Stützstellen einer Funktion eingegeben, gemäß derer die Werte transformiert werden. Der Funktionseingang ist jeweils der Systemzustand entsprechend seinem Zweck (also z.B. aktueller Wert bei Zwecke Funktion, Bilanz bei Bilanz (ohne Zielwert) oder die prozentuale Abweichung bei Bilanz (mit Zielwert)). Die Funktion kann als Treppenfunktion interpretiert werden oder zwischen den Stützstellen kann linear interpoliert werden.
Möchte man keine Transformation vornehmen, kann die Kennlinie entsprechend als 1:1 Funktion definiert werden. Wichtig hierbei ist, dass der gesamte mögliche Wertebereich eingeschlossen ist, da ansonsten für Werte kleiner der ersten Stützstelle der y-Wert der kleinsten Stützstelle verwendet wird und bei Werten größer der ersten Stützstelle jeweils der y-Wert der größten Stützstelle. Außerdem muss hier zwingend die Option Stützstellen interpolieren gesetzt werden.
| X-Wert | Y-Wert |
|---|---|
| -10000 | -10000 |
| 10000 | 10000 |
Möchte man für die Erstellung der Betriebsregeln Konstanten definieren, kann man das ebenfalls über die Option Kennlinie tun:
| X-Wert | Y-Wert |
|---|---|
| 0 | 20 |
| 1 | 20 |
Jahresgang
Bei der Option Jahresgang wird für verschiedene Zeitabschnitte des Jahres jeweils eine Funktion mit einer Stützstelle definiert. Beim konstanten Jahresgang erfolgt die Unterteilung jeweils nach Monaten, es gibt also insgesamt 12 Stützstellen. Beim variablen Jahresgang, wird an beliebigen Datumswerten unterteilt.
Pro zeitlicher Stützstelle wird jeweils ein x- und ein y-Wert eingegeben. Ist der Systemzustandswert vor der Transformation kleiner als der x-Wert wird er zu Null. Ist er größer/gleich dem x-Wert wird er zum y-Wert transformiert. Das aktuelle Datum entscheidet dabei jeweils welche zeitliche Stützstelle verwendet wird.
Standardmäßig werden die Sützstellen für den jeweiligen Zeitabschnitt konstant gehalten. Es gibt aber auch die Möglichkeit in der Zeit linear zu interpolieren.
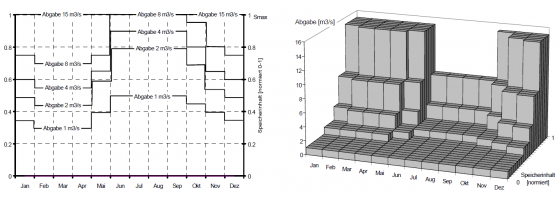
Lamellenplan
Bei der Option Lamellenplan wird klassischerweise der Speicherinhalt über das Jahr in verschiedene Bereiche (Lamellen) eingeteilt und diesen Lamellen jeweils eine feste Abgabestufen zugeteilt. Es werden also beliebige aufsteigende Abgabestufen definiert und pro festgelegtem Zeitabschnitt werden für jede dieser Abgabestufe die jeweiligen Speicherinhalte eingegeben. Die Option Lamellenplan ist aber nicht auf diese Anwendung beschränkt. Prinzipiell kann jeder beliebige x-Wert (klassisch: Talsperreninhalte) über einen Lamellenplan, zeitlich variabel in einen y-Wert (klassisch: Talsperrenabgaben) transformiert werden. Die y-Werte der Stützstellen sind dabei aufsteigend und für jeden Zeitabschnitt dieselben.
Standardmäßig werden die eingegebenen Stützstellen des Lamellenplans als Blockstufen interpretiert. Es besteht aber auch die Möglichkeit in der Zeit linear zu interpolieren und/ oder zwischen den Stützstellen der x-/y-Werte linear zu interpolieren.
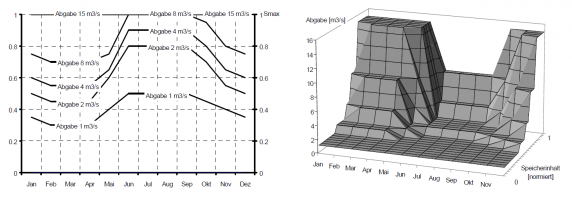
Zeitabhängige Funktion
Die Zeitabhängige Funktion ist dem Lamellenplan sehr ähnlich, aber noch ein bisschen flexibler: Die Stützstellen für die y-Werte müssen für die verschiedenen Zeitabschnitte nur in der Anzahl, nicht aber im Wert dieselben sein, zudem müssen sie nicht zwingend aufsteigend sein. Es können also für verschiedene Zeitabschnitte beliebige Funktionen mit ihren jeweiligen x- und y-Werten definiert werden.
Standardmäßig werden die eingegebenen Stützstellen als Blockstufen interpretiert. Es besteht aber auch die Möglichkeit in der Zeit linear zu interpolieren und/ oder zwischen den Stützstellen der x-/y-Werte linear zu interpolieren.
Zustandsgruppe
Eine Zustandsgruppe ist die Verknüpfung von Systemzuständen und anderen Zustandsgruppen mittels mathematischer und logischer Operatoren. Während der Systemzustand also den Zustand eines Systemelements beschreibt, bietet die Zustandsgruppe eine Zusammenfassung mehrerer Systemzustände.
Folgende Operatoren stehen für die Verknüpfung zur Verfügung:
| +/- | Addition und Subtraktion |
| ●/÷ | Multiplikation und Division |
| <>≤≥ | Vergleichsoperatoren |
| mn, mx | Minimum, Maximum |
Eine Zustandsgruppe kann aus bis zu fünf verschiedenen Systemzuständen und/oder Zustandsgruppen verknüpft werden. Da die Zustandsgruppen ihrereseits wieder weiterverknüpft werden können, besteht praktisch keine Begrenzung bezüglich der Anzahl. Dabei sind beliebige Kombinationsmöglichkeiten denkbar. Es bestehen keine Einschränkungen, z.B. hinsichtlich einer Kombination verschiedener Größen und Einheiten. Für sinnvolle Kombinationen ist der Anwender verantwortlich.
Die Systemzustände/Zustandsgruppen aus denen die neue Zustandsgruppe sich zusammensetzen soll, können bevor sie mit dem Operator verknüpft werden noch mit einem Faktor skaliert werden (s. Verbindungsfenster).
Die Zustandsgruppe selbst hat wie die Systemzustände auch das Zustandsattribut Zweck und kann mit einer Transformationsfunktion noch transformiert werden (s. Zustandsattributefenster).
Zuletzt kann die Zustandsgruppe noch in ihrem Wertebereich eingeschränkt werden (s. Verbindungsfenster).
Steuerlogik
Nachdem eine Regel in einer Zustandsgruppe/einem Systemzustand so formuliert ist, dass sie die gewünschte Abgabe aus einem Speicher oder die Aufteilung durch eine Verzweigung beschreibt, wird die Zustandsgrupppe/ der Systemzustand an das entsprechende Systemelement angeschlossen. Abhängigkeiten zwischen verschiedenen Abgaben können entweder bereits über die Definition der Zustandsgruppen abgebildet werden oder über die Option Interne Abhängigkeiten direkt im Speicherelement.